Reading Vibrating Wire Sensors: Time-Domain Analysis The traditional time-domain approach used to determine the wire’s resonant frequency
Reading Vibrating-Wire Sensors: Time-Domain Analysis
The traditional method for reading vibrating-wire sensors analyzes the response from a sensor as a function of time using period averaging. This technique excites the wire and measures the average time between a predetermined number of positive-slope zero crossings in the wire’s response to give the wire’s resonant period. Fig. 4 demonstrates this process. The resonant frequency is the reciprocal of resonant period.
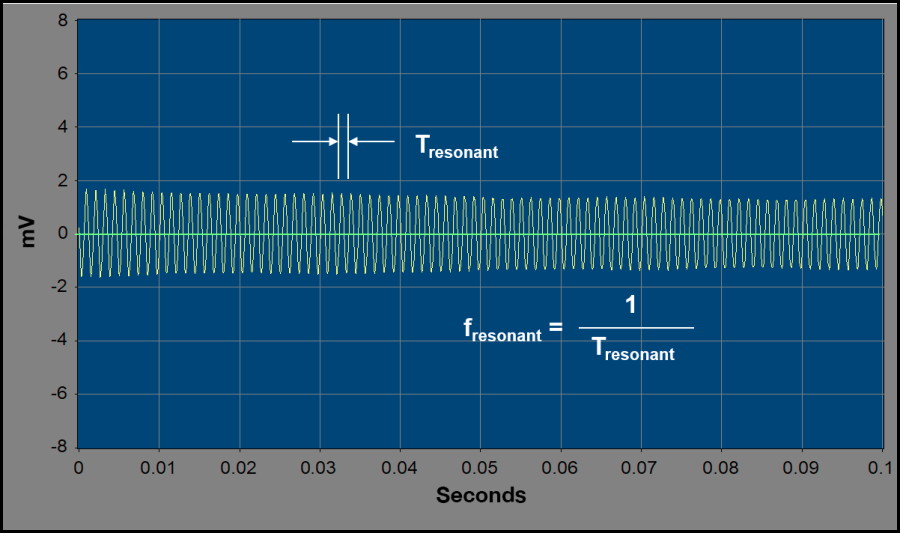
In a low-noise environment, this is an effective method of determining the resonant frequency of the wire. It has been successfully integrated into many data-acquisition products that simplify its application with dedicated hardware modules, programming instructions, and software. This approach struggles, however, in noisy environments, as shown by the erroneous readings in Fig. 1.
Fig. 5 shows the problem of measuring zero crossings in the presence of external noise.
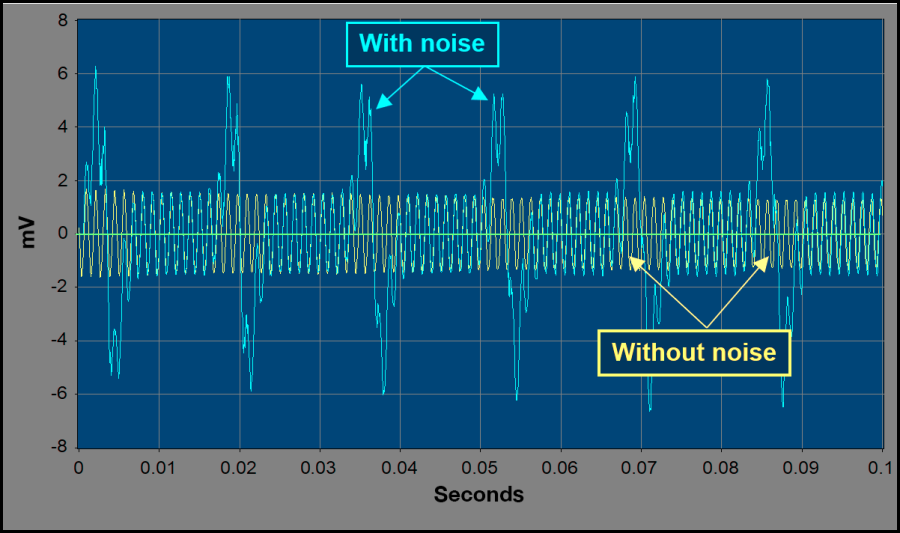
The external noise disrupts the signal, erroneously removing zero crossings. In general, external noise may introduce errors by adding zero crossings to, or by removing zero crossings from, the uncorrupted signal. Even with this difficulty, engineers are sometimes able to gather useful data in noisy environments. However, this requires extra effort to eliminate noise sources or schedule measurements around periods of increased noise. An alternative approach requires data analysts to identify and discard bad data by comparing measurement data before and after noise events.
Given these challenges, instrumentation engineers set out to find a method to determine the resonant frequency of vibrating-wire sensors with improved noise immunity.